Dimensional analysis
It is sometimes possible to work out the form of an equation simply from a knowledge of the quantities involved and their units. In such cases there is only one combination of the quantities that will give a quantity with the correct units. This method is called dimensional analysis, because physicists define about the base quantities of the SI system (mass, length, time etc.) as dimensions, but it is equally possible to do the analysis with the units themselves.
Example: - mean speed
For example the Maxwell-Boltzmann distribution of speeds contains the mass of the particle m, its speed v, the temperature T and the Boltzmann constant k. The mean speed (rms speed, most probable speed) must therefore be a function of m, k and T. What combination of these quantities can give something with the units of speed?
The method is to multiply together the dimensions (or units) of m, k and T raised to some unknown powers, and to work out what those powers must be in order to give a speed. The units of m, k and T are kg, kg m-2 s-2 K-1 and K respectively. Hence
![]()
in which x, y and z are unknown powers to be determined.
The next stage is to equate powers of each of the base units or dimensions on each side of the equation. This can be done by inspection in the present example because m and s only appear once, and kg and K need to cancel out, but it is sometimes necessary to do it formally, for example
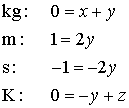
Solving,
![]()
and hence
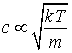
All speeds characteristic of the Maxwell-Boltzmann distribution must be proportional to this group, because this is the only way the units can be combined to make a speed. The method does not tell us the constant of proportionality, however.
Although this example is very simple, the technique is very powerful: famous examples include working out the frequency of a pendulum, or the rate of flow of a gas through a pipe (Poiseuille's equation).